Algorithme Cocke Younger Kasami (CYK)
L'intérêt de cet algorithme est de déterminer en temps polynomial si un mot donné est dans le langage L engendré par une grammaire algébrique donnée. Je peux toujours supposer que la grammaire est sous forme normale de chomsky (aussi appelée quadratique ).
J'appelle L(T) le langage engendré par la grammaire en prenant la variable non terminale T comme axiome de la grammaire.
1-Principe
2-Algorithme
BEGIN
for i:=1 to n do
Vi,1:={ A / A ---> a est une règle et la ième lettre de x est a}
for j:=2 to n do
for n:=1 to n-j+1 do
begin
Vi,j:= l'ensemble vide ;
for k:=1 to j-1 do
Vi,j:=Vi,j U {A / A ---> BC est une règle, B est dans Vik & C est dans Vi+k,j-k};
end
END
3-Grammaire de l'exemple
Variables non terminales :
S,A,B,C
Alphabet terminal : a,b
Axiome de la grammaire : S
Règles de cette grammaire
:
4-calcul détaillé sur le mot baaba
4.1 Calcul des Vi,1
l'ensemble Vi,1 est constitué des variables T telles que le sous-mot de longueur 1 commençant à la lettre i (c'est à dire la ième lettre) soit dans L(T). D'où la première ligne du tableau :
 |
1 | 2 | 3 | 4 | 5 |
| b | a | a | b | a | |
| 1 | B | A,C | A,C | B | A,C |
| 2 | ? | ? | ? | ? | X |
| 3 | ? | ? | ? | X | X |
| 4 | ? | ? | X | X | X |
| 5 | ? | X | X | X | X |
Conseil : prendre un feuille et refaire ce tableau.
4.2 Calcul des Vi,2
l'ensemble Vi,2 est constitué des variables T telles que le sous-mot de longueur 2 commençant à la lettre i ( ces mots sont baaba, baaba, baaba, baaba ) soit dans L(T).
k=1=j-1,
Rappel :
baaba : V1,1={B} et V2,1={A,C}, V1,2 est l'ensemble des T tel que T---> BA ou BC, donc V1,2={A,S}
baaba, pareil : V4,2={A,S}
baaba : V2,1={A,C} et V3,1={A,C}, V2,2 est l'ensemble des T tel que T---> AA ou AC ou CA ou CC, donc V2,2={B}
baaba : V3,1={A,C} et V4,1={B}, V3,2 est l'ensemble des T tel que T---> AB, CB donc V3,2={C,S}
D'où la deuxième ligne du tableau :
|
1 | 2 | 3 | 4 | 5 |
| b | a | a | b | a | |
| 1 | B | A,C | A,C | B | A,C |
| 2 | A,S | B | C,S | A,S | X |
| 3 | ? | ? | ? | X | X |
| 4 | ? | ? | X | X | X |
| 5 | ? | X | X | X | X |
4.3 Calcul des Vi,3
l'ensemble Vi,3 est constitué des variables T telles que le sous-mot de longueur 3 commençant à la lettre i ( ces mots sont baaba, baaba, baaba ) soit dans L(T).
k=1 correspond au découpage x / xx, k=j-1=2 correspond au découpage xx / x.
Rappel :
baaba, k=1, V1,1={B} et V2,2={B}, l'ensemble
des T tel que T---> BB est vide
k=2, V1,2={A,S} et V3,1={A,C}, l'ensemble des T tel que
T---> AA ou AC ou SA ou SC, cet ensemble est aussi vide donc
V1,3=vide
baaba, k=1, V2,1={A,C},
V3,2={C,S}, l'ensemble des T tel que T---> AC ou
AS ou CC ou CS est {B}
k=2,V2,2={B}, V4,1={B}, l'ensemble des T tel que T--->
BB est vide donc V2,3={B}
baaba, k=1, V3,1={A,C},
V4,2={S,A}, l'ensemble des T tel que T---> AS ou
AA ou CS ou CA est vide
k=2,V3,2={S,C}, V5,1={A,C}, l'ensemble des T tel que
T---> SA ou SC ou CA ou CC est {B} donc V2,3={B}
D'où la troisième ligne du tableau :
|
1 | 2 | 3 | 4 | 5 |
| b | a | a | b | a | |
| 1 | B | A,C | A,C | B | A,C |
| 2 | A,S | B | C,S | A,S | X |
| 3 | Vide | B | B | X | X |
| 4 | ? | ? | X | X | X |
| 5 | ? | X | X | X | X |
4.4 Calcul des Vi,4
l'ensemble Vi,4 est constitué des variables T telles que le sous-mot de longueur 4 commençant à la lettre i ( ces mots sont baaba et baaba ) soit dans L(T).
k=1 correspond au découpage x / xxx, k=2 correspond au découpage xx / xx, k=j-1=3 correspond au découpage xxx / x.
Rappel :
baaba,
k=1, V1,1={B}, V2,3={B}, l'ensemble des T tel que T--->
BB est vide
k=2,V1,2={A,S}, V3,2={S,C}, l'ensemble des T tel que
T---> AS ou AC ou SS ou SC est vide
k=3, V1,3=vide, V4,1={B}, l'ensemble des T tel que T--->
vide est vide
donc V1,4=vide
baaba,
k=1, V2,1={A,C}, V3,3={B}, l'ensemble des T tel que T--->
AB ou CB est {S,C}
k=2,V2,2={B}, V4,2={S,A}, l'ensemble des T tel que
T---> BS ou BA est {A}
k=3, V2,3={B}, V5,1={A,C}, l'ensemble des T tel que
T---> BA ou BC est {S,A}
donc V2,4={A,C,S}
|
1 | 2 | 3 | 4 | 5 |
| b | a | a | b | a | |
| 1 | B | A,C | A,C | B | A,C |
| 2 | A,S | B | C,S | A,S | X |
| 3 | Vide | B | B | X | X |
| 4 | Vide | A,C,S | X | X | X |
| 5 | ? | X | X | X | X |
4.5 Calcul des Vi,5
L'ensemble V1,5 est constitué des variables T telles que le sous-mot de longueur 5 commençant à la lettre i ( c'est à dire baaba entier ) soit dans L(T).
k=1, V1,1={B}, V2,4={S;C,A},
l'ensemble des T tel que T---> BS ou BC ou BA est {S,A}
k=2,V1,2={A,S}, V3,3={B}, l'ensemble des T tel que T--->
AB ou SB est {C}
k=3, V1,3={B}, V4,2={S,C,A}, l'ensemble des T tel que
T---> vide est vide
k=4, V1,4={B}, V5,1={A,C}, l'ensemble des T tel que
T---> vide est vide
donc V1,5={A,C,S}
5-commentaire
Pour chaque sous-mot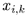 
de baaba le tableau nous dit que
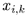le mot est dans le langage
engendré par la grammaire si et seulement si S est dans
Vi,k.
S est uniquement dans V1,2,
V3,2, V4,2, V2,4 et V1,5.
Les sous-mots ba, ab, ba, aaba et baaba sont les seuls qui sont
dans le langage, ils sont obtenus par les dérivations suivantes
:
Rappel :
S ---> AB ---> aB ---> ab
S ---> BC ---> bC ---> ba
S ---> BC ---> CCC ---> aCC ---> aABC ---> aaBC ---> aabC ---> aaba
S ---> BC ---> BAB ---> bAB ---> baB ---> baCC ---> baABC ---> baaBC ---> baabC ---> baaba
Tous
droits réservés à Hopcroft Ullman et Chrysalide
Ecrire
au webmestre