Lois de probabilités discrètes

Loi binomiale, c'est celle du tirage de boules avec remises. Si le nombre de boules noires sur le nombre de boules total
est égal à p, alors à chaque tirage, la probabilité de tirer une boule noire est p. La probabilité d'avoir tirer k boules noires au bout de n tirage est : P(X=k)=Cn,k ( p exp k ) ( (1-p) exp (n-k) ). On peut faire autre chose que tirer des boules ; les trains peuvent être en retard une fois sur quatre ou on peut tirer sur une cible dont le mille représente 10%(pourcent) de la surface sans viser.

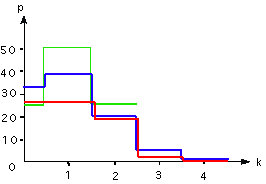
La ligne verte représente les probabilités pour p=1/2 et n=2
La ligne bleue représente les probabilité pour p=1/10 et n=10

Une première approximation lorsque p=1/n et donc 1/p=(n-1)/n, est d'utiliser la formule du binome de newton. (lorsque n est grand)

Une autre approximation est celle de la loi de poisson, si n est grand et si p=1/n, P(X=k)=1 / ( e factorielle k )

Loi de poisson, elle est définie pour tout paramètre m strictement positif, par P(X=k)=( e exp -m) (m exp k) / (factorielle k). Si n est grand et p est faible, la limite d'obtenir k boules noires au bout de n tirages avec une probabilité p suit une loi de poisson de paramètres m=np. Autrement dit, si j'ai une chance sur cent que le bus soit en retard, une loi de poisson de parmètre m=3, P(X=k) représente le probabilité que le bus ait été en retard k fois durant les 300 jours de l'année. Pour cet exemple, les calculs donnent :

k	0	1	2	3	4	5	6	7	8
pourcentage	5	15	22	22	17	10	5	2	1

Comme on le voit, cette loi est centré en 3 (et évidemment d'espérance 3).

Loi hypergéométrique, c'est celle du tirage sans remise, c'est surtout un calcul de dénombrement.

Loi de Pascal, c'est celle d'un tirage de boules avec remises, où l'on arrête l'expérience en cas de succès. Elle est défini par P(X=k)=p (1-p) exp (k-1)avec k>0. C'est par exemple celle d'ouvrir une serrure en ayant un trousseau de 10 clefs et une seule qui fonctionne et sans les différencier (mauvais exemple), c'est plutôt la probabilité de tomber enceinte au bout de k mois en ayant chaque mois une chance sur quatre ou alors la probabilité de mourir...Pour p=1/4, les calculs donnent :

k	1	2	3	4	5	6
pourcentage	25	19	14	10,5	7,9	5,9

En fait, la probabilité de tomber enceinte est plus grande que ça. De toute façon, ce qui intéresse dans les lois de pascal et de poisson, ce sont les probabilité cumulés. Avec mes exemples, la probabilité que le bus soit en retard moins de 7 fois dans l'année ( 97% ) ou d'être enceinte au bout de quatre mois ( 68,5% ), et au bout de six mois ( 82,3% ). C'est là que sont utilisés les résultats sur les séries.

Remarque : Il est équivalent de calculer les probabilités cumulées d'avoir P(X<n+1) avec la loi de Pascal (c'est à dire avoir un succès au bout de 1,2,...n fois) et de calculer P(X > 0) avec la loi binomiale de paramètre n (c'est à dire avoir 1, 2,....n succès au cours de n épreuves). Ce qui redonne d'ailleurs des égalités sur les séries et les coefficients binomiaux.

Application : le paradoxe de Walter Penney

Ecrire au webmestre

retour  à l'accueil